الخطوط العريضة للقسم

  • عام

    طي الكل توسيع الكل

  • مقدمة

    يعتبر موضوع البرمجة الخطية من أهم المواضيع المعروفة في مجال بحوث العمليات، حيث تعد إحدى الأساليب واسعة الانتشار والاستخدام للوصول إلى تحقيق الأمثلية، والتي تهتم ببناء النماذج الرياضية لحل المشاكل الاقتصادية سواء كانت إنتاجية أم تمويلية أم إدارية، فهي تساعد في تخصيص الموارد والإمكانيات المتاحة على الاستخدامات المختلفة من أجل تحقيق الأمثلية في التوزيع، كما تستخدم في جدولة الإنتاج لتحديد كميات الإنتاج المثلى، بالإضافة إلى ذلك إمكانية استخدامها في حل مسائل النقل بغية تحديد أفضل شبكة للتوزيع بأقل تكلفة ممكنة.

  • المحور الاول: البرمجة الخطية

    سنتناول في هذا المحور العناصر التالية:

    1-كيفية صياغة مسالة؛

    2-طرق حل مسالة برمجة خطية

    • تعريف البرمجة الخطية صفحة
      ينبغي للطلبة
      التأشير بأنه منجز

      مصطلح "البرمجة الخطية" مكون من كلمتين: فالأولى"البرمجة" تعني تخطيط الأنشطة أو استخدام الأساليب الرياضية للوصول إلى أفضل الحلول، أما الثانية "الخطية" فتعني أن جميع الدوال في النموذج أو العلاقات تكون خطية(رائد محمد عبد ربه؛2012،ص232) 

      وتعرّف البرمجة الخطية على أنها:"نموذج رياضي يهدف إلى تحقيق أقصى (Maximum) أو أدنى (Minimum) قيمة لدالة خطية تعرف باسم دالة الهدف (Objective Function)، وهذه الدالة مقيدة بمعادلات أو متراجحات تسمى قيودا  (Constraints)."اسماء باهرمز

    • محاضرة حول الصياغة الرياضية ملف
      ينبغي للطلبة
      التأشير بأنه منجز

      تتمحور هذه المحاضرة  حول كيفية صياغة برنامج خطي انطلاقا من نص ادبي، حيث يتم تحديد متغيرات القرار ثم دالة الهدف (قد تكون على شكل تعظيم او تخفيض)، بعد ذلك تشكيل القيود (قد تكون داخلية أو خارجية)، واخيرا نشكل القيود اللاسلبية.

    • محاضرة حول طريقة الحل البياني ملف
      ينبغي للطلبة
      التأشير بأنه منجز

      في هذه المحاضرة يتعلم الطالب كيفية رسم برنامج خطي في معلم متعامد متجانس ثم استخراج منطقة الحلول الممكنة، حيث من خلال تحديدها يمكن الحصول على الحل الامثل.

    • محاضرة مرئية حول حل برنامج خطي بطريقة الحل البياني صفحة
      ينبغي للطلبة
      التأشير بأنه منجز

      هذه المحاضرة تزيد في فهم الطالب لكيفية حل برنلمج خطي بطريقة الحل البياني

    • محاضرة في طريقة السمبلكس العادية ملف
      ينبغي للطلبة
      التأشير بأنه منجز

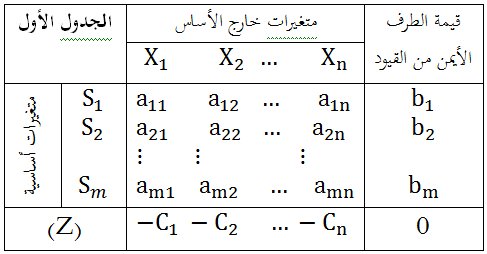
      تستعمل هذه طريقة السمبلكس في حل البرامج الخطية التي تحتوي على اكثر من متغيرين، حيث الاستعانة بمتغيرات الفرق (Si) للحصول على الجدول الاول(جدول الحل الاساسي) كما هو مبين في الجدول الموالي:

    • ينبغي للطلبة
      التأشير بأنه منجز

    • محاضرة مرئية حول طريقة السمبلكس العادية صفحة
      ينبغي للطلبة
      التأشير بأنه منجز

      في هذا النوع من السمبلكس، يشترط أن تكون دالة الهدف على شكل (Max)، وكل القيود أقل أو يساوي، كما أن الطرف الأيمن من القيود يكون موجبا، وفي حالة تحقق هذه الشروط مجتمعة نكون في سمبلاكس عادي

    • محاضرة حول طريقة السمبلكس على مرحلتين ملف
      ينبغي للطلبة
      التأشير بأنه منجز

      نلاحظ في السمبلكس العادية أن كل القيود على شكل أقل أو يساوي والطرف الأيمن موجب، لهذا تم الحصول على المتغيرات الأساسية لكل قيد بسهولة، غير أنه في الواقع قد تواجهنا بعض المسائل لا تكون فيها القيود على أقل يساوي، والطرف الأيمن من القيود قد لا يكون موجبا.

      ولمعالجة هذا الامر نلجأ الى طريقة السمبلكس على مرحلتين حيث نحاول الدخول في المرحلة الاولى الى منطقة الحلول الممكنة، بينما في المرحلة الثانية يتم البحث فيها عن الحل الامثل.

    • تمارين حول المحور الاول ملف
      ينبغي للطلبة
      التأشير بأنه منجز

      في الاخير تجدون اعزائي الطلبة مجموعة من التمارين التي تزيد فهم الطالب لهذا المقياس

    • كتاب في بحوث العمليات صفحة
      ينبغي للطلبة
      التأشير بأنه منجز

      اعزائي الطلبة يمكنكم تصفح كتاب احمد حاتم المعنون ببحوث العمليات

  • المحور الثاني: المسالة الثنوية

    إن مسائل البرمجة الخطية موجودة دائما على شكل زوجي، وبالتالي كل مسالة برمجة خطية (LP) مرفقة ببرنامج خطي مقترن معها يدعى بالمسألة الثنوية، فالمسألة الأصلية التي تتمثل في تعظيم الربح لها مسالة ثنوية تتمثل تخفيض التكاليف، والعكس بالعكس، وينتج عن المسألة الثنوية ما يسمى بأسعار الظل، وهي تمثل التغير في قيمة دالة الهدف لكل تغير قدره وحدة واحدة من كل قيد في المسألة الأصلية (الطرف الأيمن من القيد). ويتم تكوين المسألة الثنوية مباشرة من المسألة الأصلية المناظرة لها، وطبقا للنظرية الثنوية هذه فإن القيمة المثلى لدالة الهدف هي نفس القيمة الموجودة في الأصلية.

    ندعو البرنامج الخطي الأولي بالبرنامج الأصلي (P.L.Primal)، أما البرنامج الخطي المتحصل عليه في المسألة المناظرة ببرنامج الثنوي (P.L.Dual).

    ستناول في هذا المحور  ما يلي:

    1- صياغة مسالة ثنوية

    2- طرق حل مسالة ثنوية

    3- المعنى الاقتصادي لمتغيرات المسالة الثنوية

    • محاضرة في كيفية صياغة مسالة ثنوية ملف
      ينبغي للطلبة
      التأشير بأنه منجز

      تهتم هذه المحاضرة بكيفية صياغة مسالة ثنوية انطلاقا من مسالة اصلية

    • ينبغي للطلبة
      التأشير بأنه منجز

      يمكن تلخيص خطوات استخراج المسالة الثنوية من الاصلية وفق ما يلي:

      المسألة الأصلية

      المسألة الثنوية

      دالة الهدف Max(Z)

      دالة الهدف Min(Z) تحول إلى Max(-Z)

      دالة الهدف Min(W)

      دالة الهدف Min(-w)

      عدد القيود يساوي

      عدد المتغيرات (Yi)

      عدد المتغيرات (Xj) يساوي

      عدد القيود

      القيد على شكل أقل أو يساوي (≥)

      Yi ≥ 0

      القيد أكبر أو يساوي (≤) يضرب في (-1) ، أي يصبح أقل أو يساوي

      Yi ≥ 0

      القيد على شكل مساواة (=)

      Yi ≠ 0

      ونظرا لشرط اللاسلبية في المسالة الأصلية، فإن كل القيود في الثنوية تكون على شكل أكبر أو يساوي

    • محاضرة حول طرق حل المسالة الثنوية ملف
      ينبغي للطلبة
      التأشير بأنه منجز

      لحل المسألة الثنوية يمكننا استعمال خمسة طرق، وهي: طريقة التكامل بين متغيرات المسألة الأصلية والمسألة الثنوية، طريقة الاستنتاج(الحل من الجدول الأمثل للمسالة الأصلية)، طريقة السمبلاكس الخاصة بالمسألة الثنوية، وطريقة اعتبار المسألة الثنوية كمسالة أصلية يتم حلها بالسمبلاكس على مرحلتين، بالإضافة إلى طريقة الرسم البياني( في حالة وجود متغيرين).

    • محاضرة حول المعنى الاقتصادي لمتغيرات المسالة الثنوية ملف
      ينبغي للطلبة
      التأشير بأنه منجز

      تتمحور هذه المحاضرة حول كيفية شرح متغيرات المسالة الثنوية

    • لمزيد من التفصيل يرجى الاطلاع على الكتاب التالي رابط الكتروني
      ينبغي للطلبة
      التأشير بأنه منجز

      اعزائي الطلبة هذا الكتبا مفيد لكم حيث فيه بعض الامثلة وحلولها

  • المحور الثالث: مسائل النقل

    • مسائل النقل ملف
      ينبغي للطلبة
      التأشير بأنه منجز

      تعود الجذور التاريخية لتقنيات حل مسائل النقل إلى عام 1941، عندما قدم (Frank L.Hitchcock) بحثه حول تخفيض تكلفة النقل الإجمالية لعملية الشحن، ثم تناولها بشكل أوسع (T.C.Koopmans). وجدير بالذكر أن مسائل النقل تعتبر إحدى تطبيقات البرمجة الخطية، حيث تهدف إلى تقليل تكاليف نقل السلع من مصادر العرض (مراكز إنتاج، مصانع، موانئ) إلى مواقع الطلب (مراكز استهلاك، مراكز تسويق)، أو تخفيض الوقت المستغرق لعملية التوزيع، ولا يقتصر تطبيق هذه النماذج على إيجاد الطرق ذات الأقل تكلفة، بل يمكن تطبيقها على حالات يكون الهدف تعظيم العوائد الربحية إلى أقصى حد ممكن. لمزيد من التفصيل يمكنك الاطلاع على هذا الكتاب (انقر هنا)

  • المحور الرابع: البرمجة غير الخطية

    • البرمجة غير الخطية ملف
      ينبغي للطلبة
      التأشير بأنه منجز

      رأينا في المحاور السابقة أن البرنامج الخطي تكون فيها دالة الهدف وجميع القيود في صورة خطية، بينما البرنامج غير الخطي (Non Linear Programming)، ويسمى اختصارا (NLP)، تكون فيه بعض العلاقات أو دالة الهدف غير خطية.لمزيد من التفصيل يمكنك الاطلاع على هذا الكتاب(انقر هنا) 

  • ملخص المقياس

  • محتوى المقياس

  • السلاسل